本日は、ちょっとツッコミどころのある入試問題をご紹介してみます。
(問題)下図において,\(AB=AC\) である二等辺三角形ABCは円Oに内接し,円周上の点D,Eを\(AD//EB\)となるようにとる。\( ∠BAC=a\) とするとき,
\(∠DAB+∠DBA+∠EAC+∠ECA\) を \(a\) を用いて表せ。
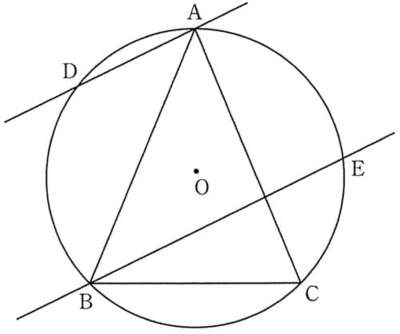
(問題ここまで)
円と角度の問題は、使いこなせるようになるべき定理がたくさんあります。しっかりと演習して慣れている生徒にとっては得点源ですが、演習量が少ない生徒は苦手にしがちな単元です。
さて、この問題のどこがツッコミどころかお分かりでしょうか。
なんとこの問題、与えられている条件のうち、\(AB=AC\) と \(AD//EB\) をどちらも用いずに解くことができてしまいます。しかも、特別なひらめきなどは必要ありません。私が普段教えている作法に従って図に書き込みをしている生徒であれば、書き込みをした瞬間にノータイムで答えが出てしまいます。
その書き込みの方法とは、「弧に円周角を書き込む」です。以下、詳しく見ていきます。
求める角度は \(∠DAB+∠DBA+∠EAC+∠ECA\) ですが、長くて見づらいので、左から順番にア、イ、ウ、エとします。求める角度は ア+イ+ウ+エ となります。以下のようになります。
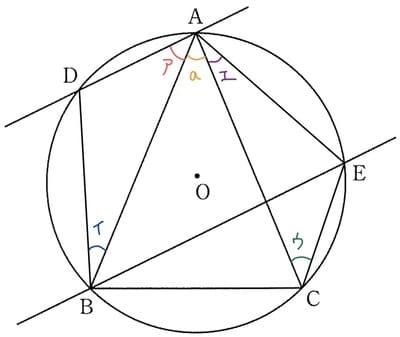
この中で、たとえばアの角度は弧DBの円周角です。それを円内だけではなく、弧にも書き込みます。←重要なポイントです。 イ、ウ、エも同様に弧に書き込むと、以下のようになります。
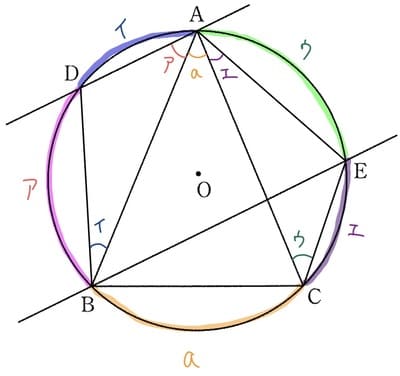
さて、弧に円周角を書き込んだことで、「円一周分の円周角は180度」という基本知識より、\(ア+イ+ウ+エ+a=180°\)が一目で分かります。
ここから、答えとなる \(ア+イ+ウ+エ=180°-a\) が分かります。
近年、難化が著しい早大本庄の数学ですが、いとも簡単に解けてしまいましたね。しかも、与えられている条件を2つも無視して解けてしまいました。
おそらく出題者側では何かしら複雑な解き方が想定されていた問題なのではないかと思います。
この問題に限らず、高校受験の数学というのは、中学受験や大学受験と比べて最も地頭的要素を必要としない、正しいアプローチさえ知っていれば解ける問題が多いと思っています。良い先生に習い、繰り返し演習して、必要な「お作法」をマスターすれば、誰でも合格点は狙えるということです。







コメント