日ごろ、「高校受験用の市販の過去問の解答解説は信用しすぎないように」と言っていますが、その一例をご紹介します。
問題
半径1の円に\(AB=1,AC=\sqrt 2\)の△ABCが内接しているとき,∠ACBの大きさは( )度であり,△ABCの面積は( )である。
問題自体は、基本的な理解を問う良問なので、受験生のみなさんはぜひ一度解いてみてから以下の内容を読んでください。
解答
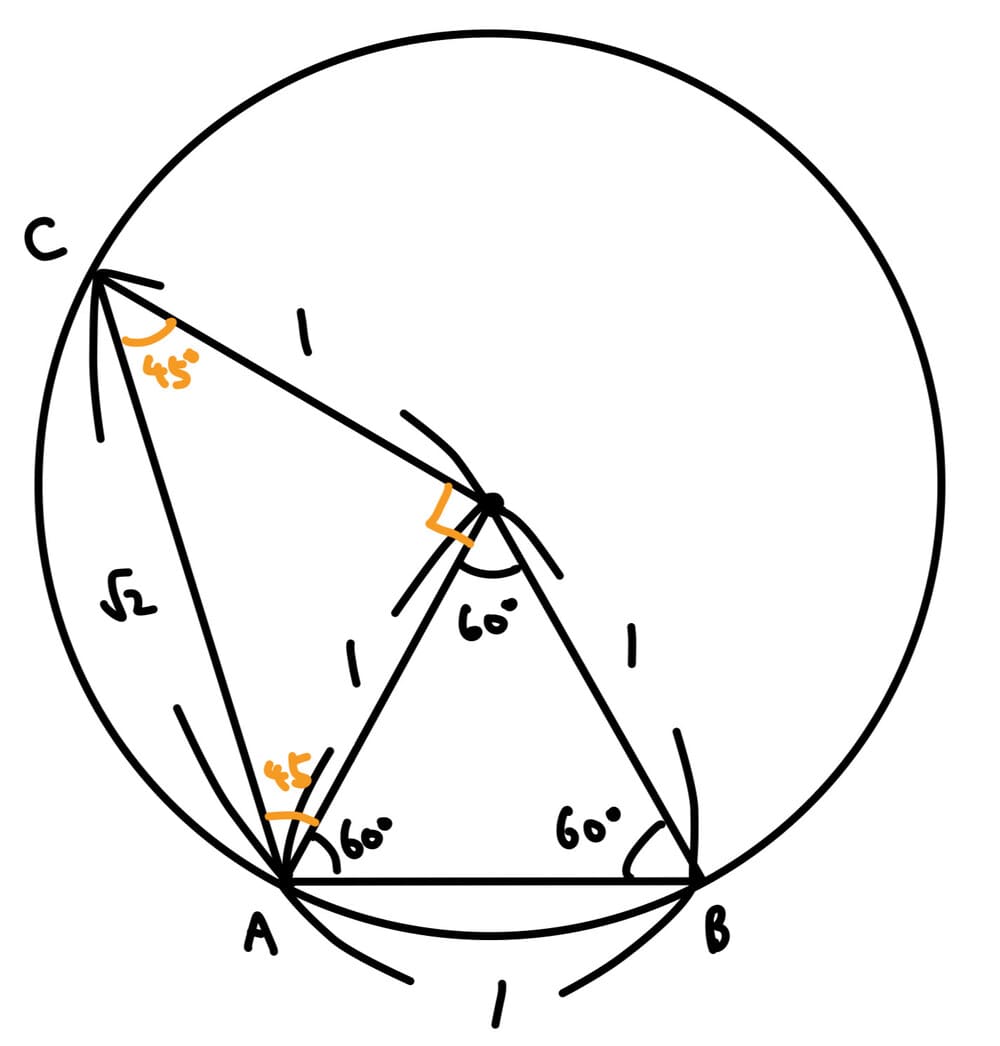
上図のようになり、∠ACBは弧ABの円周角であり、弧ABの中心角60°の半分なので、∠ACB=30°。
△ABCの面積については、
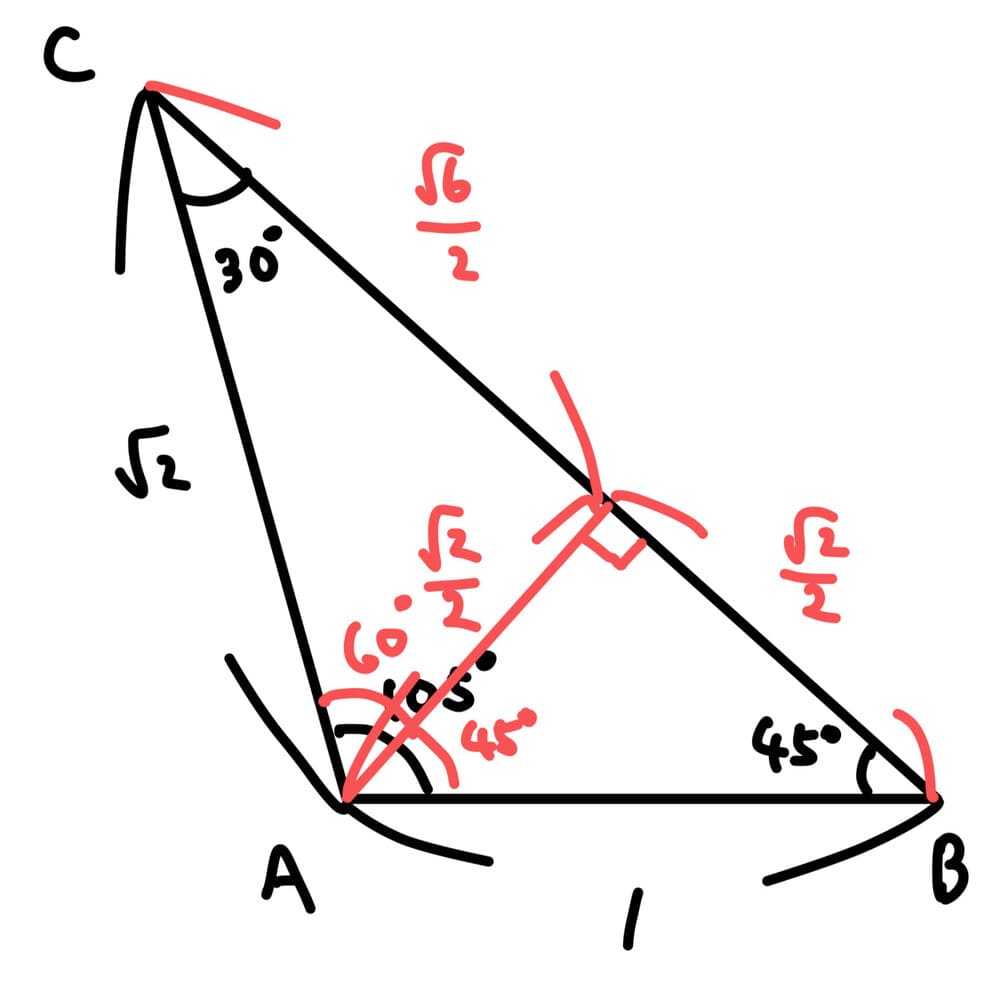
「30°と45°が特別角で、105°は要らない角」なので、105°を割るようにAから垂線を引くと、三角定規型が2個あらわれる。必要な長さを求めて、BCを底辺として面積を計算すると、\(△ABC=\dfrac{\sqrt 3 +1}{4}\)となる。
さて、解答はこれだけではないことにお気付きでしょうか。
長さ1の辺ABに対して、長さ\(\sqrt 2\)の辺ACの取り方は2通りあり、以下のような図も考えられます。
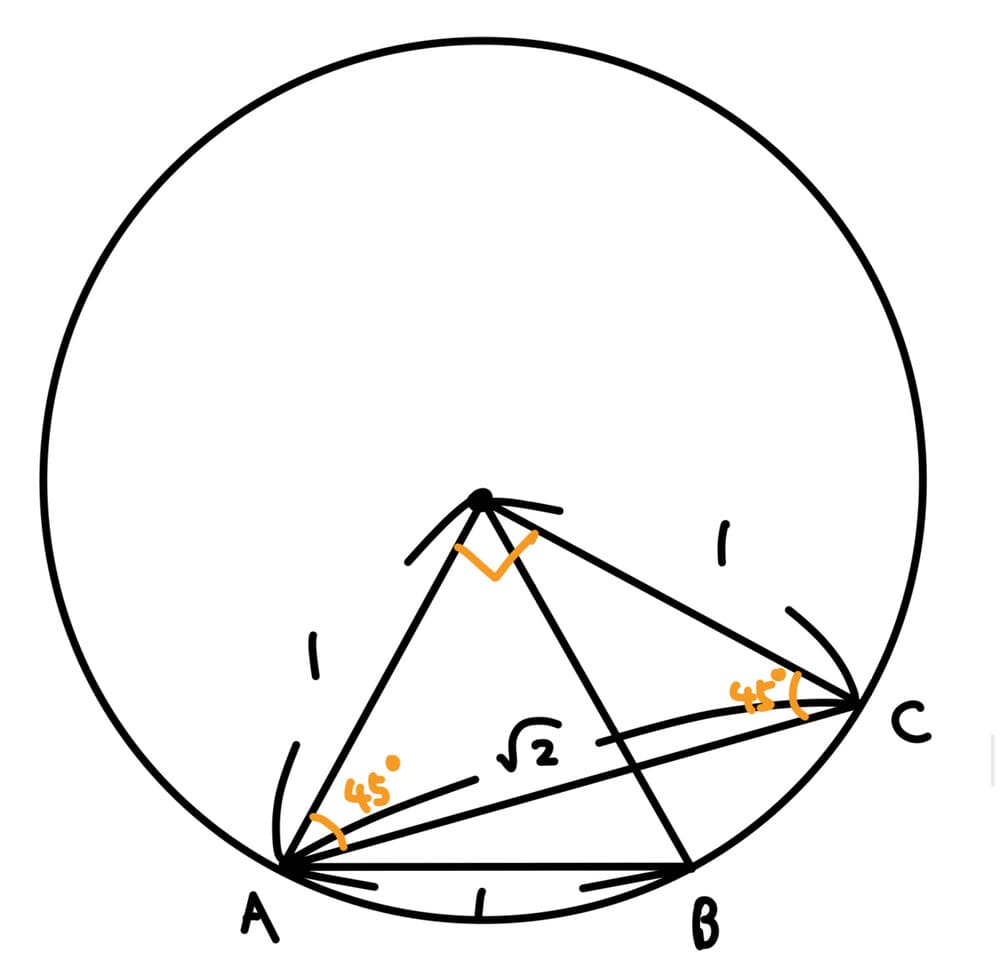
先ほどと同様に、∠ACB=30°です。
△ABCの面積については、
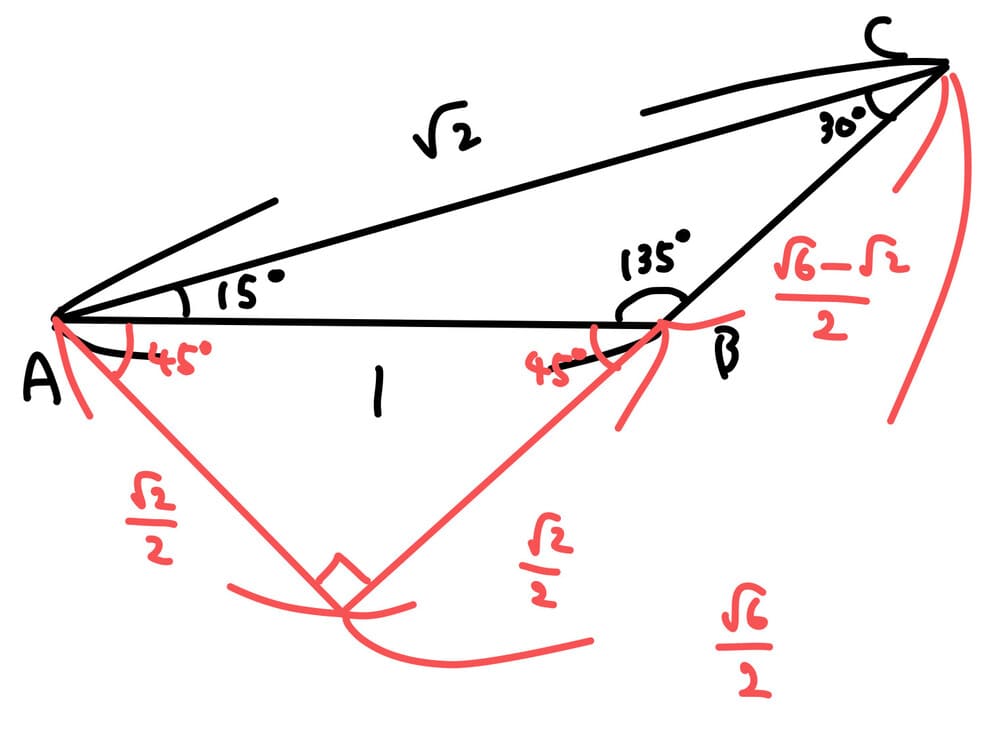
こっちはしっかり訓練していないと難しかったかもしれません。
「135°を見たら延長して垂線」までは見抜けても、右側に延長して困ってしまった人も多いのではないでしょうか。「延長して垂線」を引くとき、どうしても無意識に水平方向に延長してしまいがちです。落ち着いて、どちらに延長するのがいいかを冷静に考えてみましょう。
今回は、左下に延長することで、三角定規型が2個あらわれて、無事解くことができます。
答えは、\(△ABC=\dfrac{\sqrt 3 -1}{4}\)ですね。
実際、結構気付きづらいとは思いますので、この問題に関しては、過去問の冊子だけではなく、そもそも出題した慶應義塾高校側も、解答が2つあることに気付いていなかった可能性もあります。
慶應義塾高校は、若干そういうやらかしの多い高校ではありますので、頭の片隅に入れて受験に臨むとよいでしょう。






コメント