難しめの図形問題や連立方程式を解いていて、いくつかの条件から立式し、「これで解けるはず！」と意気込んで計算を進めていくと、「0＝0」のような無意味な式になってしまった悲しい経験がある人は多いのではないかと思います。
私も中学生の頃はよくやってしまっていました。実は、こうなってしまうのにはちゃんとした理由があります。
それを分かっていれば、0＝0が出てきてしまったときの挽回もしやすくなりますので、きちんと理解しておくことをオススメします。
0＝0が出てきてしまう具体例
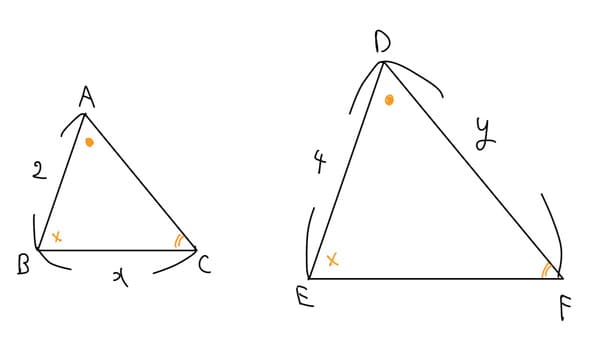
たとえば、上のような2つの相似な三角形を用いて、xやyの値を求めたいとします。（※この問題は解けないように作ってありますので、解こうとしないでください）
辺ABとDEを比べることで、相似比が1：2と分かりますから、\(EF＝x×2＝2x\)です。
逆に、ACはDFの半分になるので、\(AC＝\frac{y}{2}\)と分かります。（☆）
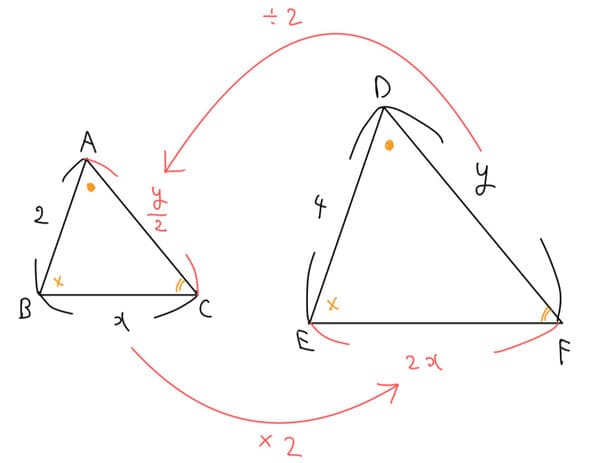
ここからもう1回相似を用いて、
\[\begin{align}
AC:BC&=DF:EF \\
\frac{y}{2}:x&=y:2x \\
\frac{y}{2}×2x&=x×y \\
xy&=xy \\
0&=0\end{align}\]となり、めでたく（？）0=0が完成しました。
0＝0になってしまう理由
ここまでの操作、なにがいけなかったかお分かりでしょうか？
なにがいけなかったかというと、「相似比1:2という同じ事実を同じ場所に繰り返し使っている」ということです。
別の言い方をすると、上の（☆）のところまでの操作で、AC：BC＝DF：EFという事実はすでに使ったのと同じ状態になっているので、そこにまたAC：BC＝DF：EFを適用しても、「そんなことは当たり前です（0＝0）」という答えしか返ってこないということです。
0＝0になったらどうしたらいいのか
ではどうしたらいいのか、ですが、その答えは「新しい事実を探しましょう」ということです。
上述のとおり、0＝0になるときは、「すでに分かっている事実を繰り返し使っている状態」です。たいていその真の原因は、「解くうえで気付かないといけない重要な事実を見落としている」ことです。
上の具体例でいえば、どこかほかの場所に二等辺三角形があるとか、別の種類の相似があるとか、なにかそういう新しい事実を見つける必要があるということです。
まとめ
「0=0」は、数学的に間違った操作はしていないが、同じ事実を繰り返し使ってしまっているので、数式に「それは当たり前だよ」と教えられている状態です。
そういうときは目の前の「0＝0」に感謝して、落ち着いて別の事実を探すようにしましょう！
コメント